Conditions Optimales
Rendement
Nous avons calculé le rendement de notre moteur, afin de savoir s'il est intéressant :
-
Le rendement est le rapport entre l'efficacité énergétique du moteur et l'efficacité théorique maximal du moteur :
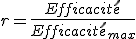
- L'efficacité d'un moteur est le rapport entre le travail et l'énergie fournie :
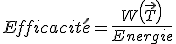}{Energie})
-
Le bateau avance à un vitesse constante de
 , la distance parcourue en 1 seconde est donc
, la distance parcourue en 1 seconde est donc 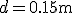
La force exercée par le moteur mesurée avec un dynamomètre est très faible, on considère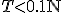
Le travail de est
est
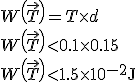 = T \times d \\ W\left(\vec{T}\right) < 0.1 \times 0.15 \\ W\left(\vec{T}\right) < 1.5\times 10^{-2} \mbox J)
-
Une bougie libère environ 42kJ en 5 minutes, en 1 seconde elle libère
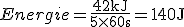


-
Le bateau avance à un vitesse constante de
-
L'efficacité maximal théorique est définie par le rendement de Carnot :
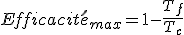
où :
 : température de la source froide, ici
: température de la source froide, ici 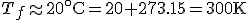
 : température de la source chaude, ici
: température de la source chaude, ici 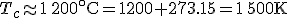
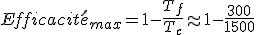
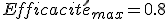

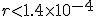
C'est très faible, lorsque l'on sait que le rendement maximal d'un moteur diesel est d'environ 45%. Il y a cependant plusieurs points améliorables.
Les paramètres
Nous avons cherché quels paramètres influençaient le fonctionnement du moteur pop pop en modifiant à chaque fois un seul paramètre et en mesurant la fréquence du moteur.
Pour mesurer la fréquence du moteur, nous avons enregistré le moteur avec un microphone et le logiciel Audacity. Nous avons obtenu le spectre du son, comme sur cet exemple :

Nous avons pu alors compter le nombre de "pop" pendant 1 seconde, la fréquence du cycle est trouvée en divisant ce nombre par deux : à chaque cycle, deux "pop", différents sur le spectre, sont émis, à l'évaporation et à la condensation.
Voici la liste des caractéristiques de notre moteur d'après nos mesures et calculs :
- fréquence (mesure) : 10 à 20 Hz
- volume de la chambre + volume des tuyères (mesuré en vidant l'eau contenue dans le moteur dans une éprouvette graduée) : 1,5 mL
- volume des tuyères (calcul) :
- diamètre : d = 3 mm
- rayon : r = 1.5 mm
- longueur : l = 90 mm
 soit 0.64 mL
soit 0.64 mL - volume de la chambre (calcul) :
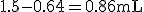
Ce calcul nous permet de prouver que toute l'eau de la chambre ne s'évapore pas : car la vapeur d'eau prend 1600 fois plus de place que l'eau liquide, et il n'y a pas de vapeur qui sort des tuyères
car la vapeur d'eau prend 1600 fois plus de place que l'eau liquide, et il n'y a pas de vapeur qui sort des tuyères - force de traction (mesure) : < 0.1 N
| paramètre | valeur | résultat | |
|---|---|---|---|
| température de l'eau | expérience témoin : | 20°C | 16 Hz |
| 7°C | 16 Hz | ||
| 60°C | 16 Hz | ||
| 80°C | 16 Hz | ||
| température de l'air | expérience témoin : | 25°C | 19 Hz |
| 35°C | 18 Hz | ||
| 55°C | 17 Hz | ||
| liquide : concentration de sel dans l'eau |
expérience témoin : | 0.00 mol.L-1 | 13 Hz |
| 4.27 mol.L-1 | 14.5 Hz |
Nous avons chauffé l'air avec un sèche-cheveux, en enfermant le bateau dans un caisson, chauffé l'eau avec un bain-marie et nous l'avons refroidit avec des glaçons. Nous avons mesuré les températures avec un thermocouple.
Il faudrait également essayer de changer la pression, la taille de la chambre, la longueur des tuyères ...
Interprétations
La température de l'eau n'influence pas la fréquence : l'eau à l'intérieur de la chambre n'est pas recyclée avec l'eau extérieur.La température de l'air semble changer la fréquence, mais il faudrait faire des mesures avec des températures plus extrêmes, de quelque degrés jusqu'à une centaine de degrés.
Quant au liquide utilisé, nous n'avons pu faire qu'un essai en salant l'eau mais il faudrait essayer avec d'autre liquides, dont les température d'ébullition sont différentes, pour avoir plus de données. Nous ne savons pas s'il faut que la température d'ébullition doit être faible ou forte.
Conclusion
Les différents paramètres que nous avons testé ne changent pas significativement la fréquence du moteur.Nous pouvons par contre essayer de modifier le moteur lui-même pour l'optimiser.
Modèles mathématiques
Nous avons mesuré la fréquence du moteur selon plusieurs paramètres. Mais en réalité c'est sa vitesse que nous cherchons. Nous avons donc cherché un modèle mathématique du moteur, une fonction qui nous permettrait de trouver la vitesse du bateau en fonction de la fréquence du moteur. Nous ne l'avons pas trouvé, mais nous pensons que la fonction ressemblerait à l'une d'entre elles :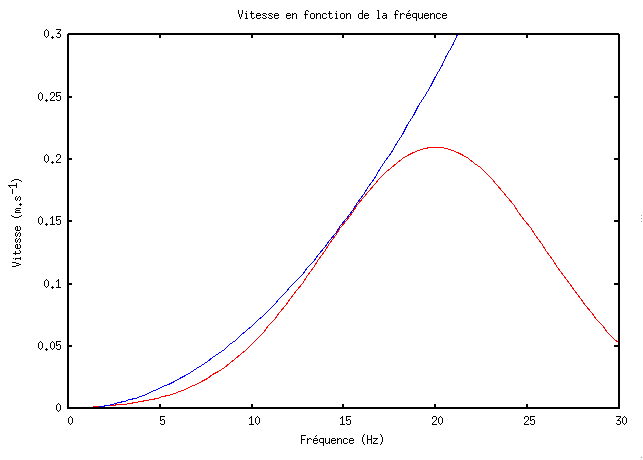
La fonction représentée en rouge présente un maximum : c'est la fréquence optimale de fonctionnement. Pour une vitesse maximale, il faut atteindre cette fréquence sans la dépassée, sans quoi le moteur ralentirait.
Conclusion
D'après ces modèles mathématiques, la fréquence doit être supérieur à 16 Hz pour que la vitesse augmente (mais inférieure à 20 Hz pour la courbe rouge). Par exemple, pour la température de l'air, le paramètre testé qui change le plus la fréquence, doit être diminuée pour accélérer le bateau.Forme générale
Le principal frein du moteur est le fait qu'il fait avancer puis reculer à chaque cycle le bateau. Orienter une tuyère vers l'avant ne changerait rien, puisque les deux tuyères ont le même rôle. Nous pouvons cependant imaginer un moteur muni de deux clapets de non-retour sur chaque tuyères :
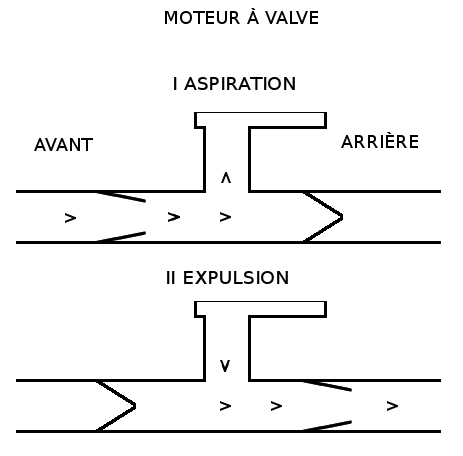
Quand le moteur chauffe et expulse de l'eau, le clapet avant se ferme et l'eau est expulsée vers l'arrière. Mais quand le moteur aspire de l'eau, c'est le clapet arrière qui se ferme et l'eau est aspirée à l'avant. Ainsi la vitesse et le rendement du moteur seraient nettement améliorés.

